The rotational motion of two uniform solid cylinders each rotating about its central axis is a fundamental concept in classical mechanics. This topic delves into the kinematics, dynamics, and energy associated with such systems, providing a comprehensive understanding of their behavior and applications.
Understanding the rotational motion of two uniform solid cylinders is essential in various fields, including engineering, physics, and manufacturing. It forms the basis for analyzing and designing rotating machinery, such as engines, turbines, and generators, and provides insights into the behavior of objects in motion.
Kinematics of Rotation

Kinematics of rotation describes the motion of rotating objects without considering the forces that cause the motion. Two important concepts in kinematics of rotation are angular velocity and angular acceleration.
Angular velocity is the rate at which an object rotates around an axis. It is measured in radians per second (rad/s). Angular acceleration is the rate at which angular velocity changes. It is measured in radians per second squared (rad/s^2).
There is a relationship between linear velocity and angular velocity. The linear velocity of a point on a rotating object is equal to the product of the angular velocity and the distance from the point to the axis of rotation.
Angular velocity and acceleration can be measured using a variety of methods, such as tachometers, stroboscopes, and accelerometers.
Dynamics of Rotation, Two uniform solid cylinders each rotating about its central
Dynamics of rotation describes the forces that cause objects to rotate. The key concept in dynamics of rotation is moment of inertia.
Moment of inertia is a measure of an object’s resistance to angular acceleration. It depends on the mass of the object and its distribution around the axis of rotation. The greater the moment of inertia, the more difficult it is to accelerate the object.
The relationship between torque, moment of inertia, and angular acceleration is given by the following equation:
τ = Iα
where:
- τ is torque (N·m)
- I is moment of inertia (kg·m^2)
- α is angular acceleration (rad/s^2)
Torque can be applied to an object to change its angular motion. For example, applying a torque to a flywheel can accelerate or decelerate it.
Energy in Rotation
Rotational kinetic energy is the energy of an object due to its rotation. It is given by the following equation:
KE = (1/2)Iω^2
where:
- KE is rotational kinetic energy (J)
- I is moment of inertia (kg·m^2)
- ω is angular velocity (rad/s)
Rotational kinetic energy can be transferred between objects. For example, when two gears mesh, the rotational kinetic energy of one gear is transferred to the other gear.
Applications of Rotational Motion
Rotational motion is used in a wide variety of applications in everyday life, engineering, manufacturing, and other fields. Some common applications include:
- Electric motors
- Generators
- Pumps
- Fans
- Wind turbines
- Gyroscopes
The advantages of using rotational motion in these applications include:
- High efficiency
- Smooth and continuous motion
- Ability to generate high torque
Answers to Common Questions: Two Uniform Solid Cylinders Each Rotating About Its Central
What is the relationship between angular velocity and linear velocity?
The relationship between angular velocity (ω) and linear velocity (v) is given by v = ωr, where r is the distance from the axis of rotation.
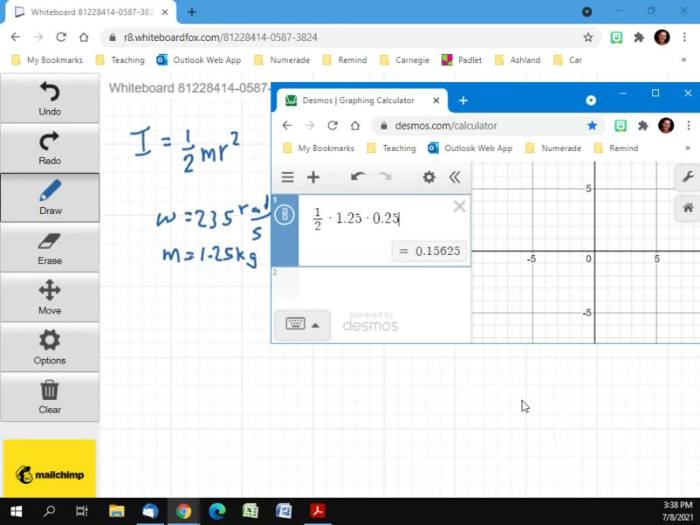
What is the moment of inertia of a solid cylinder?
The moment of inertia of a solid cylinder about its central axis is given by I = (1/2)mr², where m is the mass of the cylinder and r is its radius.
How is torque related to angular acceleration?
Torque (τ) is related to angular acceleration (α) by the equation τ = Iα, where I is the moment of inertia.